The Fibonacci Network

20 February 2021

I want to share a very peculiar graph with you. Despite its simplicity, this graph actually exhibits some very interesting behavior:

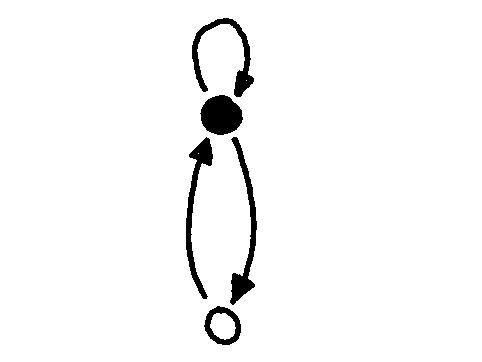
This graph has two nodes: one which I have colored black, and one which I have colored white. Between these two nodes there are two directed edges, one in each direction. And from the black node, one “self-loop” edge doubles back so that if you leave the black node via this edge, you return to where you started.

We’re going to ask the following question:

Suppose I live at the black node, and I have enough energy to walk along N edges. How many unique ways can I get back to where I started?

For example, let’s consider N = 1:

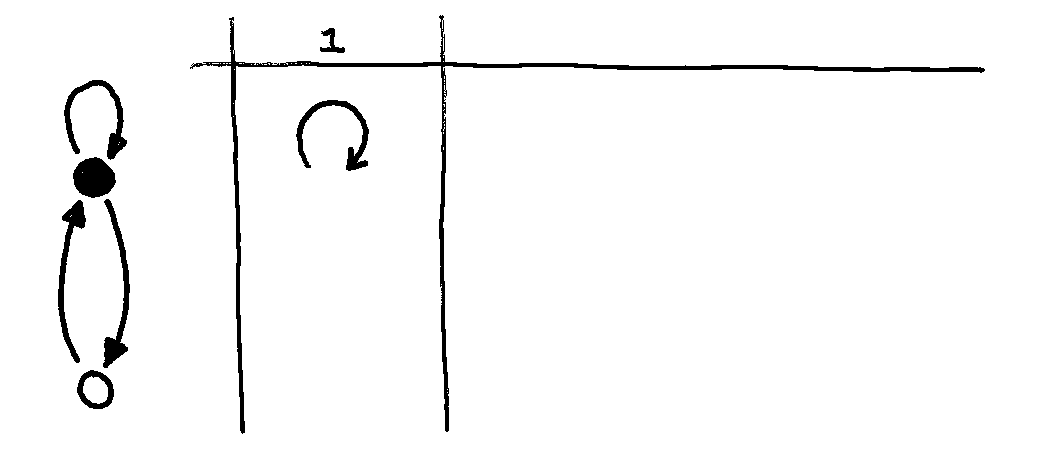
There’s only ONE path of length N=1 that gets you FROM the black node back to the black node: Namely, you have to take the self-loop.

How about paths of length N = 2?

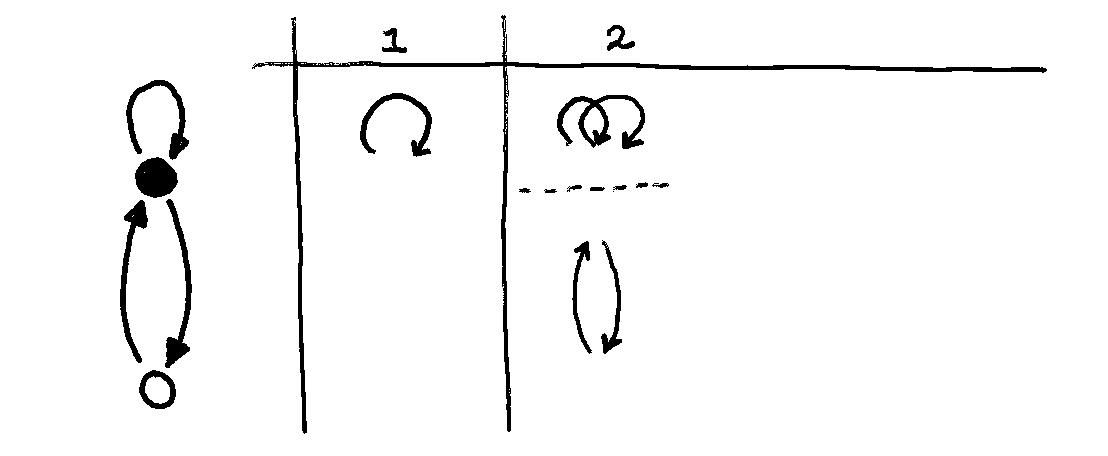
There are TWO ways to get back to where you started if you have enough energy to take two edges in your path: You can either take the self-loop twice, or you can take one hop to the white node, and then another hop back.

Let’s look at N = { 1, 2, 3, 4 }:

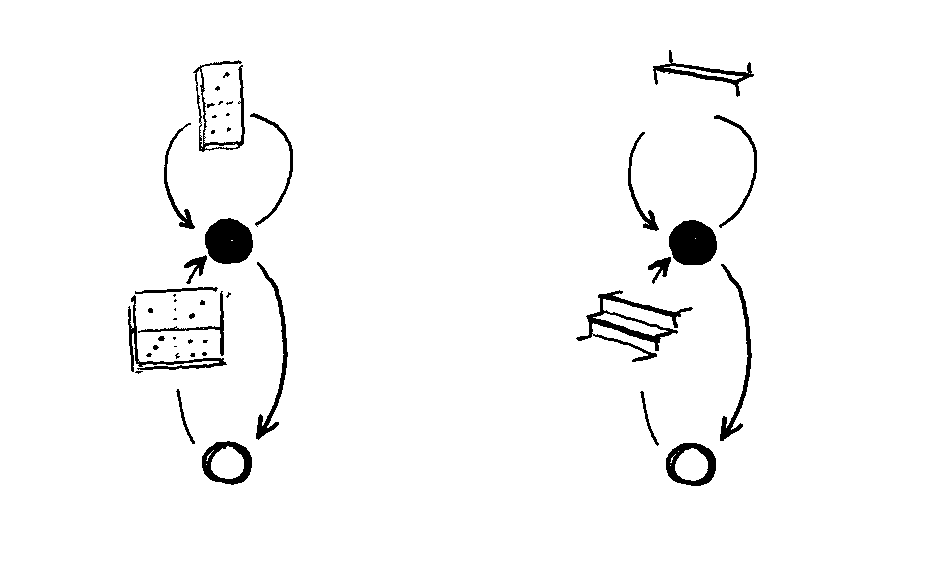
Here I’m using a loopy shorthand to illustrate a self-loop, and a V-shaped shorthand to illustrate taking the path from black to white to black again. I think they’re cute!

The first property that may seem unintuitive is that the number of options grows at all: some folks with whom I’ve shared this graph imagined that the number of paths for N = 100 would be the same as the number of paths for N = 1000.

The second property that might interest you is the rate at which the options grow:

  • There’s only 1 way to make a path of length 1 that returns home.
  • There are 2 ways to make a path of length 2 that returns home.
  • There are 3 ways to make a path of length 3 that returns home.
  • There are 5 ways to make a path of length 4 that returns home.

Our sequence is (1, 1), (2, 2), (3, 3), and then a pesky (4, 5)! Is that five a mistake?

Let’s try the next few lengths of path to see if things suddenly click into place:

On my computer, these files are all saved as “Vonnegut diagrams” because they look so much like Vonnegut’s self-portrait.

1, 2, 3, 5, 8, 13… Now it should be clear that we really ought to have started counting with all paths of length 0, so our sequence looked more like how we expect:

1 1 2 3 5 8 13 21 34 55 89 144 233 377

(See more of the Fibonacci Sequence at The OEIS)

It is very cool that we just discovered something completely novel together that has never been seen before.

JUST KIDDING!

Cassini’s Identity

This fascinating property is actually as old as dirt (technical term), and it was first published (in a slightly different form) by Giovanni Cassini in 1680.

Through the incredible Observatoire de Paris, you can actually find and read the original “Cassini Identity” text publication, though I unfortunately cannot, since I can read neither French nor Latin.

More specifically, Cassini discovered the algebraic phenomenon that

\[(F_{n-1} F_{n+1}) - F_{n}^2 = (-1)^n\]

In other words, the (n - 1)th Fibonacci number, multiplied by the (n + 1)th Fibonacci number, is equal to the square of the nth Fibonacci number, plus-or-minus 1. (Thanks u/Mathemologist for pointing out an egregious typo here!)

I’ve seen this identity manipulated in a few interesting ways, but one apocryphal manipulation (though a few sources including Wikipedia point to Knuth’s The Art of Computer Programming) is my favorite: By interpreting the left-hand side of this equation as a determenant of a 2×2 matrix, we can interpret the Fibonacci sequence through the lens of linear algebra.

Recall that the determinant is computed as:

\[det\begin{bmatrix} a & b \\ c & d \end{bmatrix} = ad - bc\]

If we plug-and-chug, we see the following:

\[det\begin{bmatrix} a & b \\ c & d \end{bmatrix} = (F_{n-1} F_{n+1}) - (F_{n} F_{n})\] \[= det\begin{bmatrix} F_{n+1} & F_{n} \\ F_{n} & F_{n-1} \end{bmatrix}\]

But make it graphs

Because I learned all of these things in completely the wrong order, I always interpret square matrices as adjacency matrices for a graph. Let’s pick the initial condition of the Fibonacci sequence (the smallest values of n):

\[\begin{bmatrix} F_{n+1} & F_{n} \\ F_{n} & F_{n-1} \end{bmatrix} \Bigg| _{n=0} = \begin{bmatrix} 1& 1 \\ 1 & 0 \end{bmatrix}\]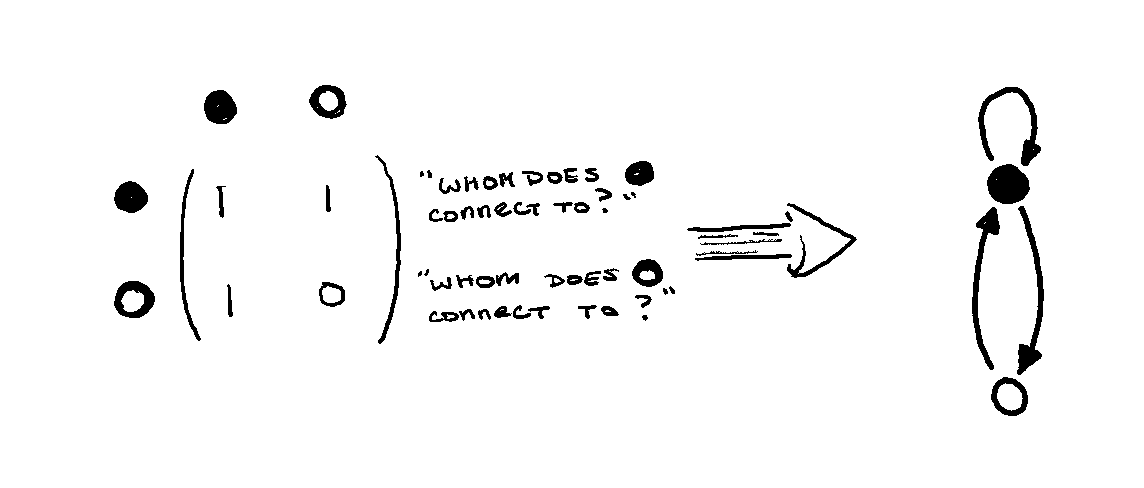

Magically, we can now see that powers of this matrix result in larger and larger Fibonacci matrices:

\[\begin{bmatrix} F_{n+1} & F_{n} \\ F_{n} & F_{n-1} \end{bmatrix}^m = \begin{bmatrix} F_{n+m+1} & F_{m+n} \\ F_{m+n} & F_{n+m-1} \end{bmatrix}\]

For example, to get things started:

\[\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^2 = \begin{bmatrix}2 & 1 \\ 1 & 0\end{bmatrix}\] \[\begin{bmatrix}2 & 1 \\ 1 & 0\end{bmatrix}^2 = \begin{bmatrix}3 & 2 \\ 2 & 1\end{bmatrix}\]

And so on.

But we’re not just doing this because it feels nice! Taking powers of graphs’ adjacency matrices means something in the graph-math sense. The diagonal entries of an adjacency matrix to the nth power are the counts of paths that start and end at that node with length n.

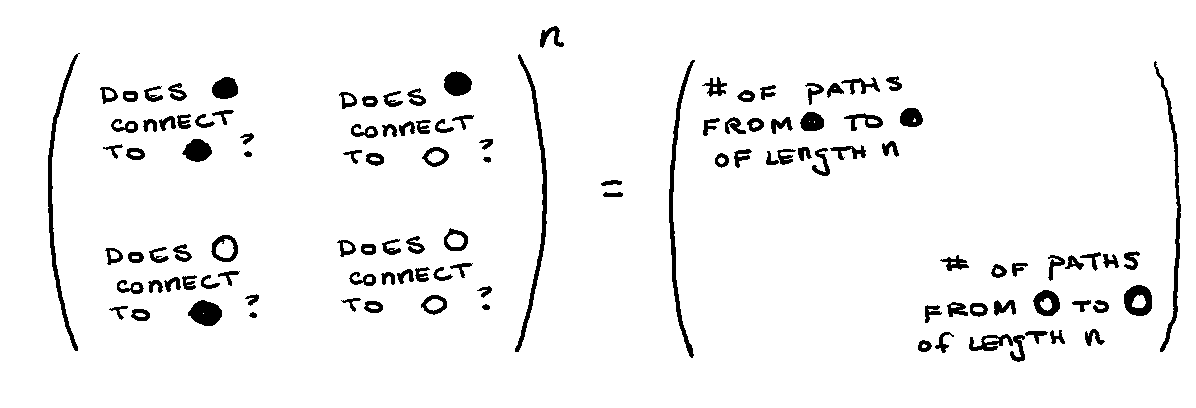
And so we get back to where we started at the beginning of this article: With thanks to Cassini, we can generate the Fibonacci sequence just by walking around on this specially designed graph.

As far as I can tell, this cute graph property is a new interpretation of the Cassini identity, though I’m convinced it’s probably scrawled somewhere on a graduate student’s whiteboard, and just never merited actual publication.

I hope it was as fun a surprise to you as it was to me! It also begs the question: Are there variants of this graph that form other interesting sequences?

Graph walks are notoriously computationally expensive, so it’s unlikely this will suddenly show us a magical new way to efficiently compute sequences that we hadn’t thought of before. But it’s always exciting to see an old phenomenon pop up in a new place. The Fibonacci Network — who would have guessed?

Updates!

Thank you to Math-Twitter for some amazing explanations and pointers, including this Structure Function Calculator by @kjoshanssen! I love a good visualization, and this is that :)

@littmath also demonstrates how the Fibonacci network maps nicely to domino tiling on the 2×n grid, and @weebiloobil comments on how this maps nicely to the total number of ways to go down an N-step staircase 2-at-a-time or 1-at-a-time.

I’m thrilled to suddenly find myself in much deeper math waters than I expected after following some breadcrumbs in the responses to my tweet about this article — thank you!

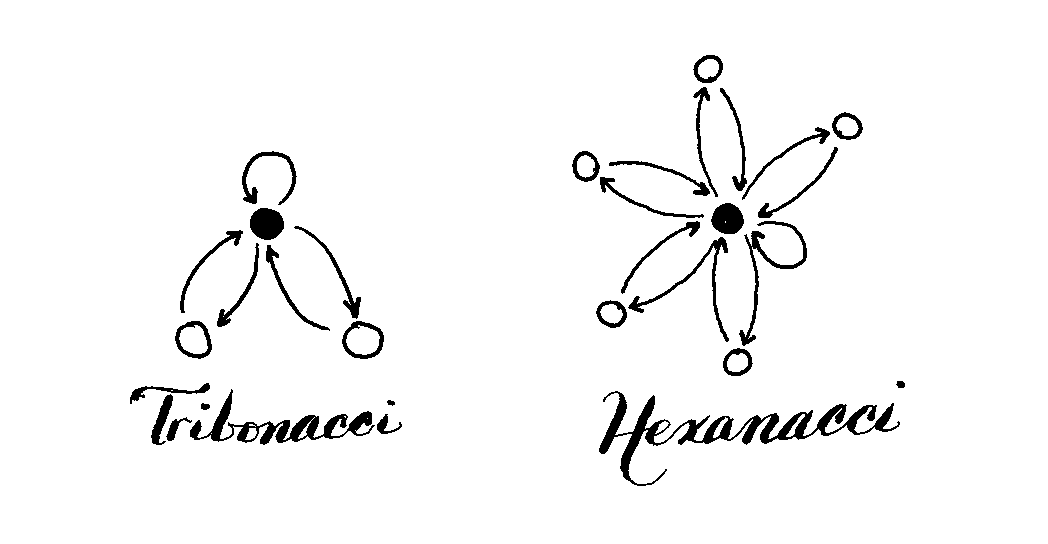
Redditor u/and_i_want_a_taco requested Hexanacci Vonnegut diagrams, and I couldn’t resist:

In the post, I discuss higher-order Fibonacci networks:

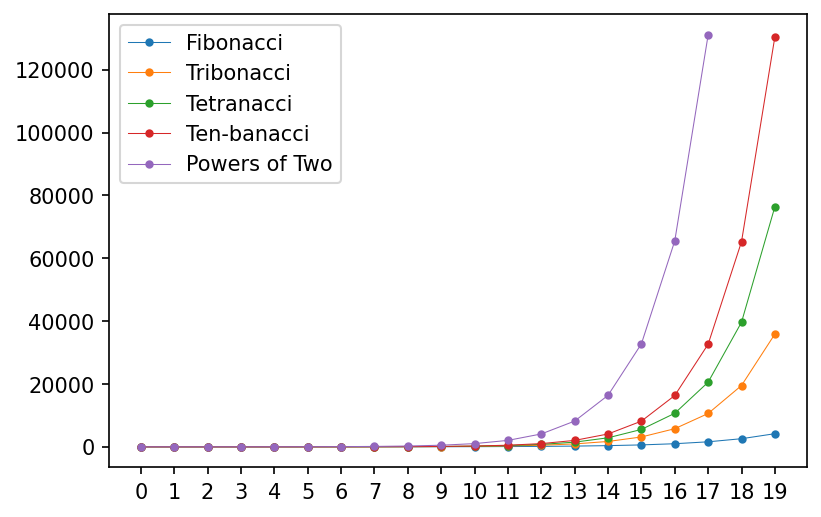
As a parting gift, I wrote a tiny snippet of Python code (using the networkx library) to perform these walks “the slow way.” You can run the code for yourself through MyBinder: Binder

Here are the results of Tribonacci, Tetrabonacci, and Decinacci sequences:

Written on February 20, 2021
Comments? Let's chat on mastodon (Or on Twitter if you absolutely must...)